Aan sommige redeneringen lijkt een onweerstaanbare logische kracht ten grondslag te liggen. In dergelijke gevallen volgt de stelling onverbiddelijk uit de premissen; als je de laatste aanvaardt, lijkt het rationeel gezien onmogelijk de eerste niet ook te aanvaarden. Zie het onderstaande voorbeeld:

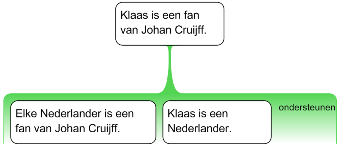
Figuur 2.20

Als je aanvaardt dat elke Nederlander een fan is van Johan Cruijff en je aanvaardt dat Klaas een Nederlander is, moet je ook aanvaarden dat Klaas een fan is van Johan Cruijff. Anders gezegd, het is onmogelijk dat Klaas geen fan is van Johan Cruijff als hij een Nederlander is en alle Nederlanders fan zijn van Johan Cruijff. Deze relatie tussen de premissen en de stelling wordt geldigheid genoemd. Een redenering is technisch gezien geldig als de stelling niet onwaar kan zijn als de premissen waar zijn.

Als je goed naar het voorbeeld kijkt, zal het je opvallen dat het even goed werkt voor Piet als voor Klaas. We kunnen zelfs alles over Nederlanders en Johan Cruijff weglaten. Dan zien we dat het niet om de betekenis van de gebruikte termen gaat, maar om de logische structuur van de redenering:

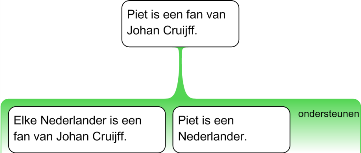
Figuur 2.21

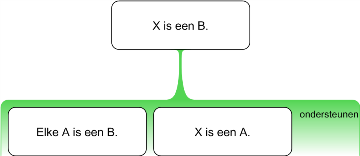
Figuur 2.22

De oorspronkelijke redenering is volkomen overtuigend, ook als je niet weet wie Klaas is, omdat de logische vorm de afleiding van de stelling lijkt te garanderen.

Een deductieve redenering is een redenering die geldig is dankzij haar logische vorm.

Anders gezegd probeert een dergelijke deductieve redenering je van de premissen naar de (hoofd)stelling te dwingen louter door de manier waarop de redenering is opgezet. Als de structuur correct is en je de premissen aanvaardt, kun je niet anders dan ook de stelling aanvaarden. Is de structuur niet correct, dan heb je te maken met een ongeldige deductieve redenering.

Deductieve redeneringen spelen een zeer belangrijke rol in de logica en verwante vakgebieden zoals wiskunde en informatica. Een groot en vaak zeer technisch subgebied van de logica, de formele logica, is gewijd aan het onderzoek van deductieve redeneringen.

Deductieve redeneringen komen we vaak tegen in de gesprekken van alledag, maar in het algemeen gaat het daarbij om een beperkt aantal typen. De meeste redeneringen die we in het dagelijks leven gebruiken, zijn niet deductief. Als we vast willen stellen in welke mate de bijbehorende stellingen worden gegarandeerd, moeten we niet alleen naar de logische vorm kijken; we moeten ook weten wat de betekenis is van de gebruikte termen en daarbij moeten we kennis hebben van het gebied dat door deze termen wordt beschreven. Met de meeste dagelijkse redeneringen wordt geen geldigheid nagestreefd; het is veeleer de bedoeling om de aanvaardbaarheid van de stelling te verhogen dan om deze te garanderen. Er zijn veel soorten niet-deductieve redeneringen, maar we hebben het meestal over inductieve redeneringen (waarbij gebruik wordt gemaakt van extrapolatie of generalisatie) en abductieve redeneringen (waarbij het gaat om het geheel of gedeeltelijk verklaren van gegevens).

Zie ook:

• Basisbegrippen Redeneerpatronen, Inductieve redenering, Abductieve redenering en Drogreden
• Wiki bij Rationale: http://www.reasoninglab.com/rationale-wiki/